Introduction

In July 2002, I went to the European Spreadsheet Risks Interest Group conference in Cardiff. After arriving early and discovering the shops hidden away in Cardiff's Victorian shopping arcades, I decided to buy a few items in order to make a point at the conference. Marker pens, fluorescent card, safety pin and a pair of 1970s-retro flared trousers: result, worn with the trousers, one badge proclaiming "Spreadsheets have not evolved since flares were last in fashion".

This was prompted by the thought that, although the past 25 years have brought us 1024 x 768 hi-res screens instead of VT52 terminals, visual interfaces to Visual Basic, and Microsoft's ubiquitously obsequious paperclip, they have done little to solve the problem of spreadsheet errors. As the identity of the Cardiff conference organisers indicates, spreadsheeting is as error-prone as ever. Excel pays more attention to graphics than to fundamental programming problems. But on the other hand, it also occupies an honourable place in computing, being, as our feature on Extending the Concept of Spreadsheet explains, the world's most widely used functional language. You can spreadsheet in Scheme; hypertext guru Ted Nelson related his multidimensional ZigZag hypertext toolkit to spreadsheets; and researchers are busy extending spreadsheets with constraint programming and logical rules.

Because of their importance, we have devoted this month's issue to spreadsheets and AI. On the risks side, we have a feature on my Model Master, a program which uses Prolog to reduce spreadsheet errors. We look at neural nets and cellular automata in Excel. And we have items by Mike Kassof from the Stanford Logic Group about his work on logical spreadsheets, and by Dennis Merritt on Amzi!'s ARulesXL, which by embedding logical rules in Excel, makes possible applications that are not practical using Excel on its own.

Extending the Concept of Spreadsheet

Scheme In a Grid

Scheme In A Grid, or Siag, is a spreadsheet written by Ulric Eriksson in Scheme. It looks not unlike Excel, and formulae can be entered in Excel notation. But they can also be entered in Scheme. For example, A1+B1 could be entered as (+ a1 b1). In fact any Scheme function can be called in a formula, including Siag's cell-access functions such as (href N) which returns the contents of the cell N rows up. This makes it convenient to do things which Excel would do only awkwardly with macros or Visual Basic. And Siag is not limited to numbers and strings, but can compute with the full range of Scheme datatypes.

Siag is part of Siag Office, a free Linux office package which includes a word processor, animation program, and editor, Although Eriksson's on-line documentation says that Siag stands for "Siag Is Not An Excel Emulator", some of its built-in functions are designed to be Excel-compatible. Since Siag is open-source, these might be useful to readers needing to emulate parts of Excel.

Spreadsheets in functional languages

Older than Siag - dating from 1985 or so, it may be the first spreadsheet to go beyond numerical calculations - is Aaron Sloman's VCalc. Sloman wrote this in Pop-11, one of the languages making up the Poplog system. Although written as an experiment, VCalc was used for some serious tasks, such as allocating limited computing connections between competing groups of users, subject to various constraints. One feature was a constraint checker which could run arbitrary Poplog code - for example, an expert system could be invoked!

VCalc is not grid-based, but uses declarations in a file read by Poplog's Ved editor to indicate where cells are to be displayed. This is excusable in a mid-1980s program running on cursor-addressable terminals; with modern Poplog graphics, a much better version could be written.

Scheme and Pop-11 are both "functional" languages, meaning that computation is expressed as function calls. They are also said to be "impure", because they contain loops, side-effects, and other non-functional features. In this, they contrast with the "pure" functional languages such as Haskell and Miranda. Because these lack side-effects, researchers have had to devise ways for them to express input-output, coming up with the notion of "monads". Functional-programming enthusiasts may be interested to hear that monads can be used to implement the immediate update-on-cell-change needed by spreadsheets, using techniques described in papers by Magnus Carlsson and by Umut Acar, Guy Blelloch and Bob Harper. Check out the links for details.

Spreadsheets as functional languages

Many people do not realise that Excel spreadsheets are functional programs. Of course, the Excel engine isn't - it's probably implemented in some Microsoft dialect of C. But the formulae a user puts into its cells are. Write them as equations, and this becomes obvious:

A1 = 3
A2 = A1-32
A3 = A2 * 5/9

The only computation is by function calls. This is of more than theoretical interest. Functional languages are much easier to reason about and analyse than imperative languages, a fact that should cheer those developing spreadsheet debugging and error-detection tools.

User-defined functions in Excel

Although Excel is a functional language, it is a strange one: it doesn't allow users to define their own functions. As Simon Peyton Jones, Margaret Burnett and Alan Blackwell say in their paper Improving the world's most popular functional language: user-defined functions in Excel:

From a programming language point of view, then, spreadsheets lack the most fundamental mechanism that we use to control complexity: the ability to define re-usable abstractions. In effect, they deny to end-user programmers the most powerful weapon in our armory. Can you imagine programming in C without procedures, however clever the editor’s copy-and-paste technology?

They propose an extension to Excel which permits this, whereby users define functions on separate worksheets, using some cells as formal parameters. This may interest those designing end-user spreadsheets and spreadsheet-like programs such as truth-maintenance systems. But what's important is the authors' use of empirical studies of programmers and research into the psychology of programming: As they say:

Despite the deficiencies of spreadsheets when they are considered as programming languages, it is clear from their commercial success that people find them useful and usable. This is not true to the same extent of any traditional programming language. Why not? One contributing factor may be that, although programming languages are a channel of communication between people and computers, most programming-language research is devoted to the computer end of the channel. Comparatively little research considers the people who do the programming. It is our belief that programming language design projects should adopt a more usercentered approach, in order to maintain a sharp focus on the people who are intended to benefit from the new language features or environments being created. This is the approach that we have adopted in our own work on extending spreadsheet capabilities.

The authors use the notions of "Cognitive Dimensions" and "Attention Investment", two structured approaches to human issues in programming developed by human-computer interaction researchers to help computer scientists, who are not usually cognitive psychologists.

Cutting spreadsheets into strips and gluing them into loops: ZigZag, GZigZag, Gzz, and Fenfire

A different way to broaden the spreadsheet concept, which I discovered when reading Chris Browne's excellent Linux Spreadsheets page, is ZigZag, invented by hypertext guru Ted Nelson. He describes it as:

resembling nothing else in the computer field that we know of, except perhaps a spreadsheet cut into strips and glued into loops.

ZigZag cells can lie in a space of any dimensionality, not just two. Dimensions have user-definable names: a list of people might have one dimension for year of birth, one for first name, and one for last name. Each dimension would contain the same cells, but they could be ordered differently: for example, ordering first names and last names alphabetically, and years of birth numerically. As this shows, we can regard dimensions as labeled lists of cells.

Within each dimension, a cell can have only one immediate neighbour on each side: one "up" neighbour and one "down". If a cell is in more than one dimension, it may have different neighbours in each: my "down" neighbour in the first-name dimension might be a John Smith (my name is Jocelyn), while in the last-name dimension, it could be Olaf Palme. ZigZag researcher Tuomas Luuka explains this with diagrams in A Gentle Introduction to Ted Nelson's ZigZag Structure. In a different example, he suggests representing trees (in the computing sense) in ZigZag by having one dimension that connects a node to its parent, and another that connects siblings of the same node.

ZigZag follows two axioms: all connections must be two-directional; and to preserve visualizability, no cell should have an enormous number of connections. These restrictions make it easy for end-users to build hyperstructures by arranging data along various dimensions of classification. They avoid dangling pointers, since all links are two-directional; and they make it easier to display data. Finally, they simplify programming, which - Nelson hopes - will encourage applications programmers to share data across application boundaries.

The most recent implementation is Fenfire. This began as GZigZag, an open-source ZigZag implemented by Lukka and colleagues working with Nelson. GZigZag changed to Gzz after Nelson asserted his trademark on the "ZigZag" name, and changed again to Fenfire after he asserted his patent on the ZigZag data structures: Fenfire has switched to RDF.

It's worth reading Hyperstructure: Computers built around things that you care about, by Lukka and Benja Fallenstein. They explain how Fenfire displays RDF as a "focus+context graph". Unlike with other RDF browsers, users can turn off relationships they don't want to see. A nifty extension of these ideas is FenPDF, a tool for structuring collections of academic articles, using "buoys" to anchor one document to those connected to it.

I wonder whether the Fenfire browser will ever reach the level aspired to in a Lambda the Ultimate posting. Under the heading Nelson, "CrackMonkey" reminisces:

Ted Nelson handed me one of the original diskettes, wrapped in a triangular origami pouch of grey letter paper (complete with egregious claims and a high-contrast image of Ted's face). It was at a party in the Presidio of San Francisco, and he demonstrated it to partygoers by showing how you could set up a genealogical database using its N-d spatial rotation from link axis to link axis.

He said that he imagined a chair with two joysticks: one navigated the 2-D space you saw on the screen, and the other controlled which relationships the X and Y axes represented. It is quite a novel interface, and could be useful for LDAP browsers or other database query tools.

I still have the paper triangle, but the diskette seems to have slipped out long ago.

Two-dimensional programming languages

One message - shapr's roughly Turing machine + Spreadsheet in that Lambda the Ultimate thread points out that GZigZag cells could hold code as well as data. Its scripting languages usually used the cells like a Turing machine tape, making it possible to emulate TheBrain, wikis, or any sort of personal Web.

I don't know whether this has any practical use, but one can also embed and execute code in a two-dimensional grid, creating a two-dimensional machine code. The languages Befunge and Orthogonal implement this idea; Francis Irving's Excel implementation of Orthogonal actually sits inside a spreadsheet. As he says:

The program counter can move not just right, but left, up and down as well This makes loops neat - they are natural, and don't require that the program counter should jump.

His page includes an Excel spreadsheet which implements Orthogonal, sample programs, and a screenshot showing Orthogonal machine instructions inside a workbook. He speculates that Orthogonal might be important for artificial life, perhaps as an extension of Thomas Ray's Tierra. This famous Artificial Life program featured one-dimensional creatures made of mutatable machine code that lived and reproduced inside a virtual machine. They evolved as Tierra ran, setting off an evolutionary arms race which gave rise to parasites, immunity to parasites, hyper-parasites, social hyper-parasites, and hyper-hyper-parasites.

Logical spreadsheets

Let's return now to extending spreadsheets' formula languages. Researchers in the Logic Group at Stanford are developing technology for "logical spreadsheets". In their version of a logical spreadsheet, the formula language is expanded from function definitions to general logical constraints.

Unlike traditional spreadsheets, logical spreadsheets can propagate values in any direction. For example, one might specify a start time for a room reservation along with an end time, and the duration of the reservation would automatically get filled in. Alternatively, one could specify the start time and the duration, and the end time would automatically get filled in. In addition, the logical constraints can express many-to-many relationships instead of just functional ones. For example, the start time for a reservation does not functionally determine the end time, though it does constrain it, since an event cannot end before it starts!

Another example of a many-to-many constraint is a constraint mapping between cities and ZIP codes. One could select Oklahoma City, OK as the city and constrain the possible ZIP code choices to the 78 ZIP codes found in the Sooner State capital, or choose ZIP code 73513 and constrain the possible cities to Oklahoma City, OK and Moore, OK.

Michael Kassoff, a PhD student in the Stanford Logic Group, has provided us with an interactive example of a logical spreadsheet:

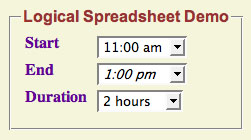
The example, for which a screen shot is shown above, contains three cells - start, end, and duration, as in the scenario above. It also contains two logical constraints. The first constraint says that the start time is before the end time. The second says that the start time plus the duration is the end time.

E > S WHEN start(S) AND end(E)

E = S+D WHEN start(S) AND duration(D) AND end(E)

Play around with the example. Try entering 9:00 am as the start time. Now, open up the end time menu, and notice that 7:00 am, 8:00 am and 9:00 am are colored red to indicate that they are incompatible choices. Then choose 1:00 pm as the end time, and the duration will be automatically filled in as 4 hours. The duration is italicized to indicate that it is a computed value rather than one entered directly. Now remove your choice of 1:00 pm for the end time by choosing the empty value (the top choice) from the menu, and choose a value for the duration. Note that the end time is automatically filled in.

Logical spreadsheets can sometimes resolve conflicts automatically. For example, if you choose 9:00 am for the start time and then choose 8:00 am for the end time, the start time will be automatically erased because it is inconsistent with your choice of end time. Alternatively, a spreadsheet can keep the inconsistent values but alert the user to the problem. As an example, try entering a start time of 9:00 am, an end time of 1:00 pm, and a duration of 1 hour. These three choices are incompatible, so the spreadsheet indicates this problem by coloring the three choices red.

The idea of a logical spreadsheet is not entirely new. In the 1980's, several systems were developed that added Prolog rules to traditional spreadsheets, namely Frank Kriwaczek's LogiCalc spreadsheet, Maarten H. van Emden et al.'s unnamed system, and PERPLEX, created by Michael Spenke and Christian Beilken. In addition, over the last 15 years or so, the field of interactive constraint solvers has sprung up, beginning with Sanjay Mittal and Brian Falkenhainer's paper on Dynamic Constraint Satisfaction Problems in 1990. Logical Spreadsheets can be regarded as interactive CSPs in which the constraints are given in a logical language.

Logical spreadsheet technology is rapidly being transferred from academia to the commercial world. Last year, Professor Michael Genesereth approached the Defense Advanced Research Projects Agency (DARPA) in hopes of finding funding for Stanford's work on logical spreadsheets. Those talks led to DARPA issuing a Small Business Innovation Research grants call for proposals on "deductive spreadsheets." Four companies were granted initial Phase I funding, including Prolog guru David Warren's company, XSB. Other companies have jumped on the bandwagon too, for example the Prolog shop Amzi!. Stanford also has a patent pending on Logical Spreadsheets, which is available for licensing to some interested company. Can it be too long before logical spreadsheet technology is on your desktop?

Interested in learning more about Logical Spreadsheets? Check out Stanford's site: logic.stanford.edu/spreadsheet/.

Links

General

dssresources.com/history/sshistory.html - A Brief History of Spreadsheets, by D. J. Power, DSSResources.COM.

www.aci.com.pl/mwichary/computerhistory/articles/spreadsheets/tenyearsofrowsandcolumns - Ten Years of Rows and Columns, reprinted from Byte issue 13, 1989. The sidebar Beyond "What-if?" ends by predicting that as spreadsheet debugging improves, "Ultimately, you will use AI techniques to ask why something surprising happened in your spreadsheet". If only.

linuxfinances.info/info/spreadsheets.html - Linux Spreadsheets by Christopher Browne. The title undersells this well-informed page, which also discusses history, extensions such as Improv and ZigZag, and open-source spreadsheets.

www.faqs.org/faqs/spreadsheets/faq/ - Russell Schulz's comp.apps.spreadsheets FAQ.

web.engr.oregonstate.edu/~erwig/FOS/ - Home page for the International Workshop on the Foundations of Spreadsheets, Rome, 2004. Links to slides and the proceedings. The papers are aimed at improving spreadsheet reliability, and include work on spreadsheet semantics, analyses of spreadsheet use, and type-checking to detect errors.

Siag and VCalc

siag.nu/siag/ - Ulric Eriksson's Scheme In A Grid site. The documentation, including screenshots, is at siag.nu/online-docs/siag/siag.html.

linuxplanet.com/linuxplanet/reviews/4054/2/ - The StartX Files: Between the Sheets with Siag. Brian Proffitt's review for LinuxPlanet.

www.cs.bham.ac.uk/research/poplog/doc/pophelp/vcalc - Documentation for VCalc, as a Poplog HELP file. The source (which Aaron Sloman tells me should still run) is at www.cs.bham.ac.uk/research/poplog/v15.6/v15.6/pop/packages/teaching/auto/ved_vcalc.p.

Spreadsheets in other functional languages

www.codecomments.com/message341581.html - CodeComment archive of a discussion on spreadsheets, Haskell, and dataflow languages. Searching Usenet for "spreadsheets" together with keywords such as "logic", "dataflow", "functional" will find many other discussions and implementations.

www-2.cs.cmu.edu/~umut/papers/popl02.pdf - Adaptive Functional Programming by Umut Acar, Guy Blelloch and Bob Harper, Carnegie Mellon. They introduce "adaptive computation", a technique used in functional programming to maintain the relationship between functions' inputs and outputs as their input changes. The paper gives an efficient ML implementation.

www.cse.ogi.edu/~magnus/Adaptive/ - Adaptive - Incremental Computations in Haskell, by Magnus Carlsson. The page links to a Haskell download which uses an implementation based on Acar et al.'s, and which includes a spreadsheet demo. Carlsson explains this in his Monads for Incremental Computing, also linked from this page.

www.mrtc.mdh.se/projects/Haxcel/ - Haxcel: A Spreadsheet Interface to Haskell. Johan Malmström's MSc project page, including downloads. The "publications" link is broken, but there's a slideshow at www.mrtc.mdh.se/projects/Haxcel/download/pres.pdf.

203.162.7.79/ieee/pdf/disk_94/3466/10212/2_10_A%20FCCM%20for%20dataflow%20(spre.pdf - A FCCM for dataflow (spreadsheet) programs, by Art Lew and Richard Halverson, University of Hawaii. Explains how dataflow programs written as spreadsheets can be transformed into field-programmable gate arrays.

www.csse.monash.edu.au/~davida/papers/ActiveSheets.pdf - ActiveSheets: Super-Computing with Spreadsheets, by David Abramson, Paul Roe, Lew Kotler, and Dinelli Mather, Queensland University of Technology. Explains how supercomputers can use parallel evaluation to efficiently execute spreadsheets.

Extending Excel with user-defined functions

research.microsoft.com/~simonpj/projects/excel/ - New dimensions for Excel, which links to abstract and text for Improving the world's most popular functional language: user-defined functions in Excel.

ZigZag, GZigZag, Gzz, Fenfire

www.xanadu.net/zigzag/ - Ted Nelson's ZigZag page. His tutorial is at xanadu.com/zigzag/tutorial/ZZwelcome.html; this page contains his "spreadsheet cut into strips" quote.

gzigzag.sourceforge.net/ - GZigZag. See also www.nongnu.org/gzz/ct/ct.html, GZigZag - A Platform for Cybertext Experiments, by Tuomas Lukka & Katariina Ervasti. This shows various ways of viewing family trees and other structures. Lukka's A Gentle Introduction to Ted Nelson's ZigZag Structure is at www.nongnu.org/gzz/gi/gi.html.

www.nongnu.org/gzz/ - Gzz.

fenfire.org/ - Fenfire.

lambda-the-ultimate.org/node/view/233 - The Lambda the Ultimate thread on ZigZag's history: "It is a sad story. It is an infuriating story". Includes the "CrackMonkey" reminiscence, and assorted technical info.

fenfire.org/manuscripts/2004/hyperstructure/ - Hyperstructure: Computers built around things that you care about, by Benja Fallenstein and Tuomas Lukka, Hyperstructure Group, Agora Center, University of Jyväskylä.

fenfire.org/manuscripts/2004/fentwine/ - Fentwine: A navigational RDF browser and editor, by Benja Fallenstein, Hyperstructure Group, Agora Center, University of Jyväskylä.

c2.com/cgi/wiki?TheBrain - Wiki entry for TheBrain. Fun to play with is Ray Kurzweil's webBrain, linked from this entry at www.kurzweilai.net/brain/frame.html?startThought=Artificial%20Intelligence.

www.cooltoolawards.com/software/utilities/thebrain.htm - Review of TheBrain by Cool Tool Awards.

Two-dimensional programming languages

www.muppetlabs.com/~breadbox/orth/home.html - Brian Raiter's Orthogonal page. See www.flourish.org/orthogonal.html for Francis Irving's Excel implementation of Orthogonal.

mbays.freeshell.org/zedfunge.html - Martin Bays's ZedFunge page. See www.flourish.org/zbefunge/ for ZBefunge, Francis Irving's implementation using the Inform interactive-fiction compiler.

Logical spreadsheets

logic.stanford.edu/spreadsheet/ - The Stanford Logical Spreadsheet site.

www.dtic.mil/matris/sbir/sbir043/sbir300.html - The Small Business Innovation Research (SBIR) solicitation, with references.

www.nada.kth.se/kurser/kth/2D1363/projectInfo.htm - A project based on the SBIR request, at the Royal Institute of Technology in Stockholm.

portal.acm.org/citation.cfm?id=586081.586083 - A scalable method for deductive generalization in the spreadsheet paradigm, by Margaret Burnett, Sherry Yang, and Jay Summet. From ACM Transactions on Computer-Human Interaction, volume 9, issue 4, December 2002.

perso.enst.fr/~jld/papiers/pap.eao/96011601.html - XMOISE : A Logical Spreadsheet to Elicit Didactic Knowledge, by V. Bersagol, J-L. Dessalles, F. Kaplan, J-C. Marze, S. Picault. Brief paper on a logical spreadsheet, used to express mathematical statements such as "A group with a commutative operator is Abelian".

ARulesXL - Integrating Rules with Spreadsheets

Spreadsheets with their intuitive interface and internal calculation engine are excellent tools for numerical analysis. Rule-based systems with their declarative rule specifications and internal inference engine are excellent tools for decision support applications.

ARulesXL is a new product that integrates the two technologies. It uses the spreadsheet's intuitive interface for the definition of rules and provides spreadsheet functions that allow the rules to be queried from other spreadsheet cells as shown in the diagram below.

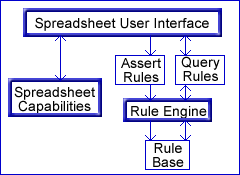
Because the definitions and queries are in spreadsheet cells, they can include references to other spreadsheet cells so that they become part of the spreadsheet's dependency graphs used for automatic recalculation. When the rules change, or values the rules depend on change, then the results of queries based on those rules are automatically updated.

The following screen shot shows an example of how telephone pricing rules can be implemented in a spreadsheet using ARulesXL (if the pictures don't show up, visit www.ainewsletter.com).

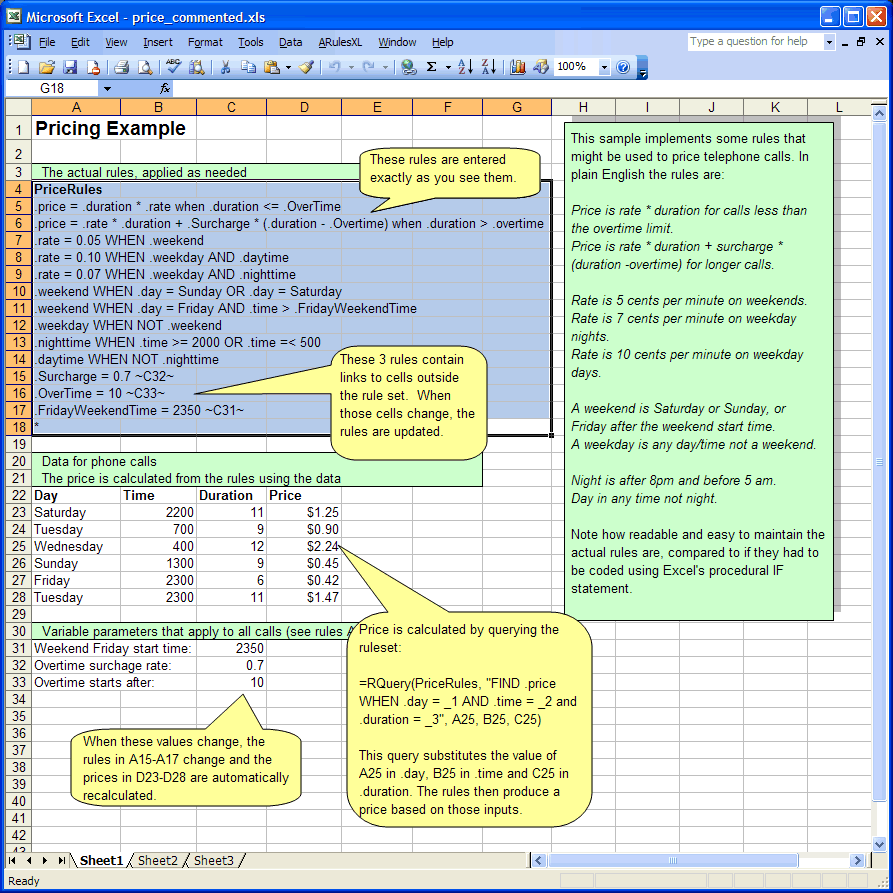
While it might be possible to implement this spreadsheet using conventional Excel IF statements, it would be difficult to write and considerably more difficult for the call pricing marketing expert to read and verify as correct.

Because the rules are clearer, they allow for the encoding, verification, and maintenance of more complex sets of business rules, making possible applications that are not practical using conventional spreadsheet capabilities alone. Applications such as taxes, human resources, benefits, work flow, pricing, underwriting, loan approval, legal advice and configuration all become viable spread sheet applications.

To learn more about ARulesXL, visit www.arulesxl.com

Numerical AI in Excel

Neural nets

I managed to find quite a few neural net spreadsheets, some of which I've linked at the end. One nice pedagogical collection, including Adaline and a Hebbian learner, has been put on the Web by Michael Dawson at Alberta, author of Minds And Machines: Connectionism And Psychological Modeling.

One of his spreadsheets is a Hopfield net. This raises a problem, because Hopfield nets model a dynamical process similar to the settling of compass needles in a magnetic field. The customary simulation requires neurons' activations to be repeatedly updated until they converge. As far as I know, such iterative processes can't be written in pure Excel. However, one can code them in Visual Basic, C, and other languages, by writing "add-in" functions that are called from formulae as though built-in, and which can use loops and recursion to do iterative calculations. Details can be found in most Excel Developers' guides.

Spreadsheets as front-ends

The add-ins idea can be taken further, so that we use Excel merely as a front-end for input and display of data (why write your own charting and graphing packages when Excel provides such a variety), delegating all calculations to functions in some other language. I mention this because there are several such programs available. One - certainly not the only one - is the nicely presented NeuroSolutions for Excel, an add-in that interfaces Excel to NeuroSolutions's neural network simulator:

You simply highlight portions of your data as training, cross validation, or testing within your Excel spreadsheet, step through a few configuration panels, and you have a working neural network. Configure another panel and watch Excel graph the results from a batch of experiments. This powerful feature allows you to easily determine the optimum network parameters.

It's worth noting that there is another way to use Excel as a front end: inputting data to Excel, but then saving the spreadsheet to a file which is read and processed by another program. Indeed, we can save formulae into such a file as well as constant data. Should some problem be best defined as a set of equations, they could be input to Excel, saved to file, and processed in your favourite compiler-writing language. I don't know any AI programs front-ended by Excel in this way, but I did find others that are, such as StrongWare's software for modelling flow paths.

Cellular automata

Like Hopfield nets, simulating cellular automata requires iterative updating. However, if we decide in advance how many generations we want to display, there is a trick by which we can implement them without add-ins. As Chris Hand explains in his paper Simple Cellular Automata on a Spreadsheet, you have to make one copy of the cellular automaton grid for each generation. Each grid except the first contains state-change formulae in its cells: these refer to the previous grid. Excel's normal spreadsheet updating rules will then propagate state from one generation to the next. This kind of display is useful in teaching. A good example is a "small worlds" CA, on the Complex Markets site, which models a market divided into "small-world communities". Individuals communicate with their immediate neighbours, the strength of communication depending on whether the communication stays within a community or crosses from one to another.

Links

Neural nets and genetic algorithms

www.bcp.psych.ualberta.ca/~mike/Book2/Excel/index.html - Excel neural nets by Michael Dawson, University of Alberta.

www.cs.nott.ac.uk/~gxk/courses/g5aiai/006neuralnetworks/neural-networks.htm - G5AIAI - Introduction to Artificial Intelligence, by Graham Kendall, University of Nottingham. There is a link near the bottom of the page to his perceptron spreadsheet.

www.us.kanto-gakuen.ac.jp/indo/front_e.html - Simulating Theoretical Models of Decision Making by Prolog and Spreadsheet, a collection of programs by Kenryo Indo. Includes an impressive-looking Excel Hopfield net (in Japanese).

www.neurosolutions.com/products/ns/ - NeuroSolutions.

www.imagination-engines.com/databots.htm - Imagination Engines. Intriguing pages on DataBots, described as advanced adaptive organisms that live in a spreadsheet and achieve vision, attention, visual processing, novel feature detection, movement, learning, reproduction, and creativity!

www.nd.edu/~dhartvig/omsoft/ai.htm - Operations management software links to neural nets and genetic algorithms for Excel.

www.inductive.com/software.htm - More links to case-based, neural net, and genetic algorithm tools.

Excel as a front-end

www.rateintegration.com/html/user_interface.html - Spreadsheet-Based Rules. RateIntegration's PriceMaker uses a spreadsheet as a front-end for entering rules to be used in rating telecomms services.

www.strongware.com/modeling.htm - StrongWare ® for Modelling with PC Spreadsheets. StrongWare's systems modelling software uses Excel as a front-end for entering flow paths.

the-ciba.com/ - The Visual Baler spreadsheet compiler. Taking the front-end idea further, one can compile an entire spreadsheet to an equivalent program in some other language, e.g. for use on a Web server. Visual Baler was one of the first spreadsheet compilers: there are several others.

Cellular automata

www.economicsnetwork.ac.uk/cheer/ch17/hand.htm - Simple Cellular Automata on a Spreadsheet, by Chris Hand, Kingston University. Online copy of Computers in Higher Education Economics Review, Volume 17, 2005. Describes how to force calculation of successive generations in an Excel cellular automaton.

www.complexmarkets.com/cellularworld.html - Cellular automata and small-world: the Complex Markets "small worlds" CA.

Model Master - Safer Spreadsheets with Prolog

Danger - spreadsheeter at work!

A recent Slashdot posting reports that, according to both PricewaterhouseCoopers and KPMG, more than 90% of corporate spreadsheets contain material errors. With each error costing between $10K and 100K per month, one expert estimates corporate America loses in excess of $10B annually through the misuse and abuse of spreadsheets.

There are many many stories counting the costs of spreadsheet errors, some of which have been collected on the European Spreadsheet Risks Group site. In the US, eliminating such risks has become urgent because of the Sarbanes-Oxley Act. And it's not just large multinationals who are affected. SF author and critic David Langford recounts how his publishers sent him only half the royalties he was due because a call to SUM in their royalties spreadsheet omitted to total some of its cells.

Reasons for such errors include: use of alphanumeric cell names instead of meaningful identifiers; the lack of user-defined functions; no good way to reuse code from existing spreadsheets; and the difficulty of managing spreadsheets with code-control systems such as CVS. Most importantly, because few spreadsheet end-users and managers are trained in programming, they don't realise how prone we all are to make mistakes, and how vital it is to guard against them.

Spreadsheets as equations

Model Master, or MM, is a Prolog program which I wrote to make spreadsheeting safer. The idea behind it is that spreadsheets are, as our first feature explained, sets of equations. By listing and transforming these, we can make existing spreadsheets more understandable. And by going the other way, compiling sets of equations into spreadsheets, we gain the benefits of textual source code: easy to print, easy to edit, easy to reuse, easy to enter into code-control systems.

To apreciate this, look at these equations, which could come from a simple accounting spreadsheet:

A2 = 2000
A3 = 2001
B2 = 1492
B3 = 1560
C2 = 971
C3 = 1803
D2 = C2 - B2 
D3 = C3 - B3 

Notice how they become immediately clear when we rewrite them as:

Year[2000] = 2000
Year[2001] = 2001
Sales[2000] = 971 etc.
Profit[2000] = Sales[2000] - Expenses[2000]  
Profit[2001] = Sales[2001] - Expenses[2001]  
Layout Year[2000:] as A2 downwards
Layout Expenses[2000:] as B2 downwards
Layout Sales[2000:] as C2 downwards
Layout Profit[2000:] as D2 downwards

Compiling, decompiling, and structure discovery

MM contains a compiler for converting such specifications to spreadsheets. It reads the equations and layout directives, then uses the latter to allocate identifiers in the equations to cells, saving the result as a spreadsheet. This is extremely powerful, because by varying the layouts, we can map the same equations to a spreadsheet in many different ways. Thus we could compile the same three-dimensional table to vertically stacked 2-d cross-sections in one spreadsheet, to a horizontal sequence of cross-sections in another, and to one slice per worksheet in a third. It is equally easy to run data from right to left, to accomodate Hebrew and Arabic readers. An extension to the layout directives allows labels to be added, making it easy to internationalize the text in a spreadsheet.

There is also a decompiler which converts spreadsheets back to equations. When it is given layout directives, it applies the inverse mapping to the compiler. So, given my first listing and the layout directives from the second, it would generate the equations from the second listing.

If a spreadsheet has been generated by the compiler, we will know how to group and rename its cells on decompilation. However, this won't be the case for the overwhelming majority of spreadsheets. To make them intelligible, we need to discover their authors' intentions, i.e. what arrays they had in mind when coding. I call this the problem of "structure discovery".

Structure discovery and spreadsheet grammars

There are heuristics we can use to guess at a spreadsheet's implicit structure. To find out which cells belong in the same array, we can: look for regions surrounded by text or blank cells; sequences of identical formulae; and regions passed as ranges to SUM and other aggregating functions. To discover the array bounds, we can look for sequences of numbers such as the years in my listings, and for sequences of common words such as the names of months. These will often run along a row, telling the reader the subscripts associated with the cells below; or down a column, subscripting the cells to their right. To guess names for these arrays, we can use labels in neighbouring cells, especially those above or to their left.

Such heuristics can be programmed directly in Prolog, but what's nice is that we can write them more concisely by using Definite Clause Grammars. For non-Prologers, I should explain that Prolog has a special notation for writing BNF-like grammars known as Definite Clause Grammars, plus a translator to convert them a to parser. Amzi!'s tutorial on DCGs gives more details, and demonstrates with a a grammar for (simple!) English sentences:

sentence -->
    subject,
    verb,
    object.

subject -->
    modifier,
    noun.

object -->
    modifier,
    noun.

modifier --> [the].

noun --> [cat].
noun --> [mouse].

verb --> [chases].
verb --> [eats].

We can devise similar rules to search for structure in spreadsheets. This rule searches for a label (which I define as a spreadsheet cell containing text and having no dependents) with a cell containing a formula on its immediate right:

labelled_cell( L ) --> label(N), right(1), formula_cell, at(A), 
                        L is_layout [ name=N, address=A, subscript=[] ].

When this rule is applied to a spreadsheet, if it finds a labelled cell, it creates a layout structure in variable L, giving it a name field equal to the label's text, and a base address or origin which is that of the formula cell. It also puts an empty subscript into the structure, signifying that the cell stands on its own rather than being part of an array. (Cells in arrays would get subscripts indicating their position relative to the array origin.) The layout structure is the internal representation of the Layout directives shown earlier.

Prolog as a spreadsheet-manipulation language

Prolog programmers can use the Prolog top-level interpreter as an interactive interface to MM's spreadsheet predicates, with backtracking useful for returning alternative solutions. For example, the query below would find all formulae in Sheet1 whose top-level operator is a plus:

?- load( 'spreadsheet.xml', SS ),
    cell( SS, 'Sheet1', Col, Row, Formula ),
    Sub = _+_,
    subexpression( Formula, Sub ).

Here, load reads a spreadsheet file, cell looks up the contents of cells, and subexpression matches subexpressions in formulae.

MM's compiler and decompiler can be called from Prolog too. These take spreadsheets or sets of equations as arguments (MM represents a spreadsheet as a set of equations augmented with cell styles, named ranges, and other Excel stuff), as well as lists of layout structures. For example,

?- load( 'ss.xml', SS ),
    match_all( SS, labelled_cell, Layouts ),
    decompile( SS, Layouts, Decompiled ),
    show( Decompiled ).

This query reads the file ss.xml into SS, applies our labelled-cell rule as many times as it can, gathering all the layouts into Layouts, runs them backwards generating Decompiled, and displays the transformed - and, we hope, more intelligible - listing.

We also have operators for combining spreadsheets and parts of spreadsheets, making it possible to reuse them. The most fundamental are \/, which overlays two spreadsheets (the symbol is the nearest a keyboard can come to set union); >>, which shifts a spreadsheet along a vector; and - and restrict, which remove cells, ranges, and sheets from a spreadsheet:

?- load( 's1.xml', S1 ),
    load( 's2.xml', S2 ),
    S3 is_ss ( S1 restrict 'Sheet1' sub [a,c:d] ) \/
            ( S2 restrict 'Sheet1' sub b ),
    save( 's3.xml', S3 ). 

Suppose that we have two accounting spreadsheets, both containing years in column A, expenses in B, sales in C, and profit calculations in D. We want to build a new spreadsheet which uses the sales from one and the expenses from the other. As the code above shows, it's easy - we isolate columns A, C and D from the first, and B from the second, by calling restrict. We then superimpose them with the spreadsheet union operator \/. The result is saved to s3.xml.

If, for some strange reason, the second spreadsheet had its expenses running horizontally from cell A2 rightwards, we could still use them:

?- load( 's1.xml', S1 ),
    load( 's2.xml', S2 ),
    S3 is_ss ( S1 restrict 'Sheet1' sub [a,c:d] ) \/
            ( S2 restrict 'Sheet1' sub 1 ) rebase [ a2, b2, vector(1,0), vector(0,1) ],
    save( 's3.xml', S3 ). 

What's new is rebase, which maps one set of cells into another. Here, it is given the origin of the source and target cells, and the increments between cells.

The Excelsior scripting language

Until some genius equips Prolog with a telepathy interface, we can never be sure we have uncovered a spreadsheet author's intentions. We may therefore need a lot of trial and error when doing our structure discovery. To support this, it would be useful to have a user-interface similar to Mathematica and other computer-algebra systems: see The Rosetta Stone for Computer Algebra Systems for a comparison of approaches. Such an interface should give the user some way to store for later use spreadsheets, parts of spreadsheets, cell addresses, formulae, and equations generated by structure discovery. It should obviously be interactive, and should - building on what existing computer-algebra systems find most usable - be functional rather than logic-based, meaning that commands typed at it are treated as expressions to be evaluated, rather than Prolog queries.

In addition, although the operator notation in the previous section will be manageable to Prolog experts, it suffers from the syntactic compromises needed to make it go through Prolog's parser. For example, Sheet1 had to go in single quotes to stop Prolog treating it as a variable. To overcome these problems, MM has its own scripting language, Excelsior. This was implemented for a group of systems-admin users: the type of person who doesn't know Prolog, but is prepared to hack languages like Perl and Python. Such users can use Excelsior as a batch language for automating spreadsheet editing, in the same way they'd use Perl for string-bashing. They can also use it interactively as a "spreadsheet algebra" language for trial-and-error reverse enineering.

Reverse-engineering a cellular automaton

In the Numerical AI in Excel feature, I mentioned the small-worlds cellular automaton spreadsheet. Because it lays out 26 successive generations of its CA down one worksheet, it holds a vast amount of repetitive structure, both within each generation's grid, and from one grid to another. I experimented with MM for making this structure explicit, and found that by searching the spreadsheet for identical formulae, then grouping these into runs, and runs of runs, I could list the spreadsheet very compactly.

One such set was listed as

Sheet1[ {0} >< { 4..829 by 33 } ] = "step=".

The expression inside the square brackets specify a whole set of worksheet addresses. In it, the symbol >< denotes Cartesian product, i.e. the product of two sets. These are sets of subscripts, the first being a set of column indices (based at 0), and the second a set of row indices. As conventional, they are enclosed in curly brackets. So the equation means that the cells in rows 4, 37, 70, ... 829 of column 0 contain the label step=.

Similarly, the cells in rows 6, 39, 72, ... 831 of column 0 contain the constant 1. So do the cells in rows 4, 37, 70, ... 829 of column 2. And the cells in rows 37, 70, ... 829 of column 1 contain the relative formula R[-33]C+1. MM displays this as

Sheet1[ {1} >< { 37..829 by 33 } ] = Sheet1[ HERE, HERE - 33 ]+1

This is a very compact listing: whereas the original Excel file occupied 1.8 Mb, the MM listing was only 14K and contained 17 equations.

Using the MM compiler, we can reverse this, generating a spreadsheet from such listings, making it very easy to experiment with spreadsheet-based cellular automata.

Along the same lines, MM has been used to convert an assortment of spreadsheet-based simulations into equations which can then be reimplemented in other programming languages, including: Lumina's Analytica modelling package; Java; and numerical languages such as Fortran.

MM in finance: from category theory to billion-dollar loans

One experiment with MM, which I tried at the suggestion of UK accountant and spreadsheet expert Duncan Willamson, used it to edit accounts spreadsheets. Apparently, these often fail to balance at the end of the accounting year, because some credits or debits are wrong. Accountants rectify this by patching with corrections such as "The sales department must be noted to have spent an extra £200". (I'm not an accountant, so this explanation may not be quite right.) Making these edits in Excel would require inserting extra input rows containing the correction, then updating all cell references in the calculations sheet so that they use the corrected inputs rather than the originals. This is tedious and error-prone. However, it was easy to code the edits in Prolog.

I've also worked with a US investment bank on a much bigger application, MM as the basis of a tool for checking that the bank's spreadsheets conform to in-house style rules and that their units (money, years, months, interest rates, and so on) are consistent, and that malicious users have not tampered with local copies of certain spreadsheets.

I'll end by saying a bit about mathematics. I had the idea of MM by chance, as a result of work in a branch of mathematics called category theory. This is an important and foundational (also elegant, recursive, and highly self-similar) subject, which allows one to combine varied mathematical and computational views of the same situation, snapping them together like Lego bricks. I can't imagine, though, many people running to buy a book on Category Theory with Excel. This would be a pity, because I found the subject extremely helpful, both in inspiring MM, and in clarifying its design. Some of the investment bank spreadsheets are used in assessing loans: loans which may run to several billion dollars. With mathematics comes power.

Links

www.eusprig.org/ - European Spreadsheet Risks Interest Group. The spreadsheet mistake stories are at www.eusprig.org/stories.htm.

it.slashdot.org/article.pl?sid=05/04/24/1218239&from=rss - The Slashdot thread $10B Annual Tab for Spreadsheet Errors? (Thanks to Graham Stark for the link.)

www.ansible.co.uk/ - David Langford's site. The royalties spreadsheet problem is in his entry for 6 April 2005. (His book reviews and other pieces are nothing to do with spreadsheets, but fun to read. His novel The Leaky Establishment features the slowest Space Invaders game in the world, played, in a certain Civil Service atomic research establishment, on a teletype.)

www.inacom.com/display.aspx?page=/newsletter/sarbanesoxley.aspx - May Newsletter: Sarbanes-Oxley, Simply Put, by Dan Barker from inacom.

www.businessforum.com/SEC01.html - The Emerging Company and the SEC: The Significance of the Sarbanes-Oxley Act, by Thomas Faulhaber, The Business Forum Online.

www.dmreview.com/article_sub.cfm?articleId=1012265 - Spreadsheet Jeopardy by Richard Tanler, from DMReview. Also published in* DM Direct Special Report* for October 19, 2004.

www.amzi.com/manuals/amzi7/pro/ref_dcg.htm - Amzi!'s tutorial on DCGs.

www.univ-orleans.fr/EXT/ASTEX/astex/doc/en/rosetta/htmla/roseta.htm - The Rosetta Stone for Computer Algebra Systems, by Tim Daly, Michael Wester, Alexander Hulpke, Hans Schoenemann, Serge Mechveliani, Ayal Pinkus and Michel Lavaud.

www.duncanwil.co.uk/ - Duncan Williamson's site. Includes a presentation on good design of spreadsheets, at www.duncanwil.co.uk/spreaddes_files/frame.htm.

www-cse.ucsd.edu/users/goguen/pps/manif.ps - A Categorical Manifesto, by Joseph Goguen. Also published in Mathematical Structures in Computer Science, volume 1, number 1, March 1991. It may not make much sense to non-categorists, but I hope enough shines through to demonstrate how important the subject is.

Spreadsheet Humor

I thought I'd end with some humor. The Web does not contain many jokes about spreadsheets - but I did find some, on spreadsheet consultant John Walkenbach's site. I hope that, in return for a free mention, he won't mind me quoting a few.

If a spreadsheet were a car:

• It would crash two or three times per day for no apparent reason. The driver is often hurt, but the car itself receives no permanent damage. You'd just accept this fact, restart the car, and begin your trip again.
• Occasionally, your car would fail to restart after a crash, and you'd have to reinstall the engine. For some strange reason, you'd just accept this too.
• The oil, engine, gas and alternator warning lights would be replaced by a single warning light: "This car has performed an illegal operation."

Some Riddles:

• Q. How do you identify an extroverted spreadsheet user?

• A. He looks at your shoes when he talks to you.

• Q. Why don't spreadsheets have multithreading?

• A. The designers decided one bug at a time was enough for most users.

• Q. What is the most frequent question asked by a would-be spreadsheet consultant?

• A. "Would you like fries with that?"

Why do psychologists prefer lawyers to rats for their experiments?

• There are now more lawyers than rats;
• The psychologists found they were getting attached to the rats;
• And there are some things that rats won't do

OK, so that last joke isn't about spreadsheets. It comes from a paper by Paul Thagard and Cameron Shelley, Emotional Analogies and Analogical Inference. Such jokes are funny, they explain, because:

One of the most enjoyable uses of analogy is to make people laugh, generating the emotional state of mirth or amusement. The University of Michigan recently ran an informational campaign to get people to guard their computer passwords more carefully. Posters warn students to treat their computer passwords like underwear: make them long and mysterious, don't leave them lying around, and change them often. The point of the analogy is not to persuade anyone based on the similarity between passwords and underwear, but rather to generate amusement that focuses attention on the problem of password security.

The password analogy works because part of what makes an analogy funny is a surprising combination of congruity and incongruity. Passwords and underwear are different, so it surprises us when we find a similarity. Such similarities are particularly amusing when directed at people we dislike.
To which I might add "and things we dislike". Here's one final spreadsheet joke, The Aspiring Writer:

There was once a young man who, in his youth, professed a desire to become a great writer. When asked to define "great" he said:

"I want to write stuff that the whole world will read, stuff that people will react to on a truly emotional level, stuff that will make them scream, cry, wail, howl in pain, desperation, and anger!"

He now works for Microsoft, writing Excel error messages.

Links

cogsci.uwaterloo.ca/Articles/Pages/emotional-analogies.html - Emotional Analogies and Analogical Inference, by Paul Thagard and Cameron Shelley, Philosophy Department, University of Waterloo.

www.j-walk.com/ss/jokes/ - John Walkenbach's spreadsheet jokes.

neopoleon.com/blog/posts/434.aspx - Excel as a database. Rory Blyth's spoof on those times when, at some unfortunate point in your life as a developer, a marketing fiend hands you an Excel file crammed with "data" and demands "do something with it".

www.netzmafia.de/service/admin.html - Der Excel-Affe. If the Web contains few English spreadsheet jokes, there were even fewer in the other languages I tried. But here, for German speakers, is one of many pages telling the story of "The Excel Ape".

Summary for non-speakers: tourist walks into an animal shop, and while looking around, sees a customer order an Excel ape. It's expensive. Why? Because it can program fast, cheaply, and error-free. He sees another ape, a Web ape. This is very expensive: it can design Web sites, server-side programs, all kinds of stuff. Then he sees a third ape, which is very very very expensive, more than the other two combined. Why? "Well, I've never seen it do anything useful, but the others call it administrator".

Until next month.