February 2004
The February 2004 newsletter is really a companion piece for the January 2004 newsletter. January discussed fuzzy logic and its usefulness for control systems, and included discussions of some simple examples. This month's newsletter has the code used for the experiments in January. It is a fuzzy logic laboratory intended for modification and experimentation.
The full code for the system is included in the newsletter, but if you are interested in getting the files directly, send me an e-mail.
As always, any and all feedback is appreciated,
Code Corner
The January issue talked about fuzzy logic and described some experiments with fuzzy logic and showers. There are a number of tools available for playing with fuzzy logic, but, as usual, its always fun to create your own. This month we'll describe the fuzzy logic system built for conducting experiments with control systems. The system includes the fuzzy reasoning engine and simulation capability for testing.
The knowledge representation language used to build a fuzzy control system is frame-based, as our other rule-based systems have been (see recent newsletters for other examples). There are frames for defining fuzzy sets, fuzzy rules, normal rules, and forward chaining rules for controlling the system. We'll visit each them as we walk through the coding of the single knob shower example, described in the Jan 2004 issue.
Knowledge Representation - Single Knob Shower
Fuzzy sets are defined over a crisp domain variable. The supported set types are defined by straight lines, which work well. The options are:
- descending line, defined by the domain variable where the fuzzy membership is 1.0 and 0.0,
- ascending line, defined by the domain variable at 0.0 and 1.0,
- triangle, defined by the domain variable at 0.0, 1.0, and 0.0, and
- trapezoid, defined by the domain variable at 0.0, 1.0, 1.0 and 0.0.
Other fancier sets with logarithmic curves are possible, and could be added to the system as enhancements.
These are the input and output sets described in the January 2004 issue:
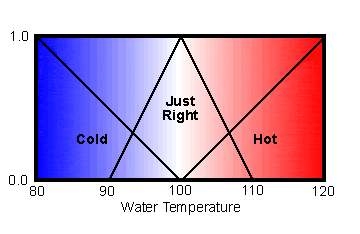
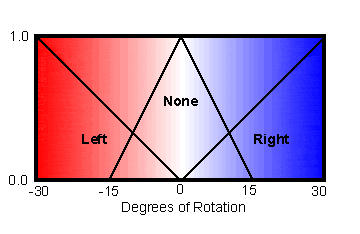
And this is how they are encoded:
fuzzy_set(water_temperature, [
variable(cold) :: descending_line( 80.0, 100.0 ),
variable(just_right) :: triangle( 90.0, 100.0, 110.0 ),
variable(hot) :: ascending_line( 100.0, 120.0 )
]).
fuzzy_set(rotate, [
variable(left) :: descending_line( -30.0, 0.0 ),
variable(none) :: triangle( -15.0, 0.0, 15.0 ),
variable(right) :: ascending_line( 0.0, 30.0 )
]).
Next are the fuzzy rules that relate the input fuzzy sets to the output fuzzy sets. They are read as: if water_temperature is hot then rotate right, etc. Note that the fuzzy rules use 'fzis' instead of is. This allows the system to support other rules as well as fuzzy ones, and also lets the fuzzy part of the system be more easily integrated into some other larger system.
The rules support: fzis (is), fzand (and), fzor (or), fznot (not) and the hedges very (square), slightly (sqrt) and hnot (not). There can be multiple rules for a single variable, in which case the results of the two rules are fzor'd together. The two knob example has more complex rules.
fuzzy_rules(rotate, [
do(right) :: water_temperature fzis hot,
do(none) :: water_temperature fzis just_right,
do(left) :: water_temperature fzis cold
]).
Normal, non-fuzzy, rules are needed for other aspects of the simulation. They are supported with a slot indicating the conditions under which they apply and the value of the variable. Sometimes the value will be computed from a formula, which is really a list of Prolog statements. Notice in this case the call to get_av/2. This is the key predicate of the system that finds a value for an attribute, triggering the reasoning engine as necessary. It would be nicer if this didn't appear in the external programming interface, as it does here, and the user could simply include a variable, say dial_angle, without having to call get_av(dial_angle, ANGLE). But that's an enhancement for a later version.
These following two rules are not really part of the control system, but are part of the simulation used to test the control system. They calculate the value of the water temperature based on the position of control. The calculation is different, depending on whether the toilet is flushing or not. A flush has the effect of making it appear as if the control is moved 20 degrees hotter.
rule(water_temperature, [
conditions :: flush = true,
formula(TEMP) :: [
get_av(dial_angle, ANGLE),
OFFSET is ANGLE -20 - (-90),
TEMP is 140 * (180-OFFSET) / 180 + 50 * OFFSET / 180 ]
]).
rule(water_temperature, [
conditions :: not flush = true,
formula(TEMP) :: [
get_av(dial_angle, ANGLE),
OFFSET is ANGLE - (-90),
TEMP is 140 * (180-OFFSET) / 180 + 50 * OFFSET / 180 ]
]).
Notice that the above math is only necessary for the simulation part of the system. If this were a real controller for a shower, the designer of the controller wouldn't have to know the equations that describe the water temperature, the real shower would provide that data.
Simpler, non-formula rules are supported too. In that case the rule just has a value. The following rule uses a variable called time_ticks which is just a counter the reasoning engine maintains for loops through the simulation. The rules indicate when the toilet is flushing. The second rule just has 'true' for a condition because it is using the fact that the rules for a given variable, in this case 'flush', are tried in the order presented.
rule(flush, [
conditions :: time_ticks > 10 and time_ticks < 20,
value :: true
]).
rule(flush, [
conditions :: true,
value :: false
]).
Control frames are used to control the simulation. Each has a condition under which it is applied, and a set of actions to take when it is applied. Notice that the conditions can refer to fuzzy variables, which need to be converted to a crisp boolean. A value of 0.8 is used as the threshold.
The first rule below fires when the water_temperature is the just_right fuzzy set is 0.8 or greater. It.simply updates the state of flush and water_temperature, and reports that all is OK. The second rule does the work when needed, first calling for an update of 'rotate'. This triggers the fuzzy rules for rotate which are based on the fuzzy sets over temperature. Having learned the rotation, the dial_angle is update by the degree of rotation, and the simulation formula for water_temperature is recalculated for the next pass through the loop.
The main control loop finds a control rule that applies, uses it, and then loops again. It is the application's responsibility to code actions, such as these, that reset the critical variables for each iteration. In this example, the flush and water_temperature are updated each cycle, and the degree of rotation is updated when changed.
control(ok, [
conditions :: water_temperature fzis just_right,
actions :: [
update(flush),
update(water_temperature),
report([`ok `, flush, ` `, dial_angle, ` `, water_temperature, ` `]) ]
]).
control(not_ok, [
conditions :: not water_temperature fzis just_right,
actions :: [
update(rotate, Rotation),
get_av(dial_angle, OldA),
NewAngle is OldA + Rotation,
set(dial_angle, NewAngle),
update(flush),
update(water_temperature),
report([flush, ` `, dial_angle, ` `, water_temperature, ` `]) ]
]).
Finally, the beginning. The start frame is used to initialize the system, and different starts can be used for different test scenarios. In is mandatory to set the test_duration, otherwise the simulation might go forever, or not at all. In this case, an initial dial_angle is chosen, on the chilly side, and the water_temperature is udpated based on it. This is then used as a start for the control loop.
start(one, [
actions :: [
set(dial_angle, 50),
set(test_duration, 30),
update(water_temperature),
report([`Start test one`, ` `, dial_angle, ` `, water_temperature, ` `]) ]
]).
Running the System
To run the system, consult, compile, or otherwise run the main/0 predicate of the fuzzy.pro reasoning engine. It will prompt for the name of a .fuz file and the name of a start scenario to use. On my system the single shower system above is called shower_1.fuz, so running it looks like this:
?- main.
Which .fuz file to run? shower_1
Which start to use? one
Start test one dial_angle = 50 water_temperature = 70
time = 0 flush = false dial_angle = 30 water_temperature = 80
time = 1 flush = false dial_angle = 10 water_temperature = 90
time = 2 flush = false dial_angle = -8.33333 water_temperature = 99.1667
time = 3 ok flush = false dial_angle = -8.33333 water_temperature = 99.1667
time = 4 ok flush = false dial_angle = -8.33333 water_temperature = 99.1667
...
time = 11 ok flush = true dial_angle = -8.33333 water_temperature = 109.167
time = 12 flush = true dial_angle = 6.42704 water_temperature = 101.786
time = 13 ok flush = true dial_angle = 6.42704 water_temperature = 101.786
time = 14 ok flush = true dial_angle = 6.42704 water_temperature = 101.786
...
time = 20 ok flush = false dial_angle = 6.42704 water_temperature = 91.7865
time = 21 flush = false dial_angle = -5.46122 water_temperature = 97.7306
time = 22 flush = false dial_angle = -8.37675 water_temperature = 99.1884
time = 23 ok flush = false dial_angle = -8.37675 water_temperature = 99.1884
time = 24 ok flush = false dial_angle = -8.37675 water_temperature = 99.1884
...
done
yes
?-
Reasoning Engine

The reasoning engine was harder to implement than I had hoped, but that was primarily because I found it difficult to find clear formulas for the centroid de-fuzzification algorithm. De-fuzzification is the process of taking the fuzzy set values on a domain and converting them to a crisp value.
The best I could find was the definition that the centroid about the x-axis, Cx, of a function f(x) was defined as the moment / area.
Cx = ò x × f(x) dx / ò f(x) dx
Its been a long time since I've had to do calculus and some of the links below are to the math sites I usedto refresh my memory. My desk was filled with bits of paper like that on the right, as I tried to remember what the integral of x squared was and how to calculate slope and intercept from points on a straight line.
I worked out the centroids for some simple shapes, and they have relatively simple formulas. For example, the centroid for a rectangle is simply the average of the two x coordinates, and for a right triangle, its 2/3 of the way towards the tall side.
But I was not able to find a simplification for the case of the centroid for the shape beneath an arbitrary line segment, and it seemed that it would be of the most general use. Here's what I came up with for how to caculate the centroid and area under a line segment (X1,Y1) (X2,Y2), where M is slope, B is Y intercept, Mx is the moment about the X axis, Cx is the centroid, and A is the area:
M is (Y2-Y1)/(X2-X1),
B is Y2 - M * X2,
A is M*X2*X2/2 + B*X2 - M*X1*X1/2 - B*X1,
Mx is M*X2*X2*X2/3 + B*X2*X2/2 - M*X1*X1*X1/3 - B*X1*X1/2,
Cx is Mx/A.
Having explained that, the rest of the code is not dissimilar from other rule-based systems described in this newsletter. Here is the rest of the code:
The operator definitions support the fuzzy operators.
:- op(950, xfx, ::). % for slots
:- op(920, xfy, or). % conventional rules
:- op(910, xfy, and). % conventional rules
:- op(920, xfy, fzor). % fuzzy rules
:- op(910, xfy, fzand). % fuzzy rules
:- op(900, fy, fznot). % fuzzy rules
:- op(700, xfx, fzis). % fuzzy rules
:- op(600, fy, very). % fuzzy hedge
:- op(600, fy, slightly). % fuzzy hedge
:- op(600, fy, hnot). % fuzzy hedge
The main entry point loads a logic base, finds the start, initializes the system and starts the control loop. An external host language using the system could emulate this code, allowing the fuzzy logic engine to be embedded .
main :-
prompt(`Which .fuz file to run? `, File),
strcat(File, `.fuz`, FuzFile),
reconsult(FuzFile),
prompt(`Which start to use? `, Start),
initialize(Start),
known(test_duration, Duration),
control_loop(Duration),
write(done),
nl.
These are the I/O statements used by the engine. They allow for the possibility that extended predicates outside of the Prolog environment have been defined to handle I/O. This would be the case for an embedded application.
prompt(Q,A) :-
ext_prompt(Q,A),
!.
prompt(Question, Answer) :-
write(Question),
read_string(Answer).
output(X) :-
ext_output(X),
!.
output(nl) :-
!, nl.
output(X) :-
write(X).
Initialize the timer, take the actions required by the start.
initialize(TEST) :-
abolish( known/2 ),
assert( known(time_ticks,0) ),
start(TEST, Slots),
get_slot(actions::Actions, Slots),
take(Actions).
The control loop is a forward chaining loop. It looks for a rule that can fire and fires it. The rule actions will cause the state of the system to change so the next time through the loop maybe a different rule will fire.
control_loop(Duration) :-
get_av(time_ticks,Duration),
!.
control_loop(Duration) :-
get_av(time_ticks,Ticks),
write(time=Ticks), tab(2),
control(_, Slots),
get_slot(conditions::Conditions, Slots),
test(Conditions),
get_slot(actions::Actions, Slots),
take(Actions),
Ticks2 is Ticks+1,
set(time_ticks,Ticks2),
!,
control_loop(Duration).
The basic utility used to retrieve slots from frames.This allows two forms of query.
get_slot(S, [S|_]).
get_slot(S, [_|Slots]) :-
get_slot(S, Slots).
get_slot(Slot, Val, [Slot :: Val | _]).
get_slot(Slot, Val, [_|SVs]) :-
get_slot(Slot, Val, SVs).
The non-fuzzy rules and the control rules have conditions under which they apply. These are the tests that are supported as conditions. The conditions can be in a list or boolean expression. Note that the last rule is a catch-all, and assumes that if none of the other test patterns applied, then the test conditions are probably fuzzy. In that case the fuzzy rule is applied and the fuzzy value that results is compared to 0.8, the criteria for absolute truth.
test([]) :-
!.
test([Condition|Conditions]) :-
test(Condition),
!,
test(Conditions).
test( C1 and C2 ) :-
test(C1),
test(C2).
test( C1 or C2 ) :-
(test(C1); test(C2)).
test( Attr = Val ) :-
get_av(Attr, Val).
test( not C ) :-
not(test(C)).
test( Attr > Val ) :-
get_av(Attr,X),
X > Val.
test( Attr >= Val ) :-
get_av(Attr,X),
X >= Val.
test( Attr < Val ) :-
get_av(Attr,X),
X < Val.
test( Attr =< Val ) :-
get_av(Attr,X),
X =< Val.
test(true).
test( Fuzzy ) :-
apply_fuzzy_rule(Fuzzy, Val),
!,
Val >= 0.8.
These are the actions that can be taken in a control rule. Note that there is a catch-all clause that allows any Prolog goal to be called as well. Given this, its not really necessary to have the other clauses, except that at some point it would be nice if there was a specific list of allowable actions, and for that the individual take/1 clauses will be perfect.
take([]) :-
!.
take([Action|Actions]) :-
take(Action),
!,
take(Actions).
take( set(Attr,Val) ) :-
!, set(Attr,Val).
take( update(Attr,Val) ) :-
!, update(Attr,Val).
take( update(Attr) ) :-
!, take( update(Attr,_) ).
take( report(Items) ) :-
!, report(Items).
take( X ) :-
call(X),
!.
take( X ) :-
output(nl),
output( error:X ),
output(nl),
fail.
clear(Attr) :-
retract( known(Attr,_) ),
!.
clear(_).
set(Attr,Val) :-
clear(Attr),
assert( known(Attr,Val) ).
update(Attr,Val) :-
clear(Attr),
get_av(Attr,Val).
report([]) :-
output(nl).
report([Text|Items]) :-
string(Text),
output(Text),
!,
report(Items).
report([nl|Items]) :-
output(nl),
!,
report(Items).
report([Attr|Items]) :-
get_av(Attr,Val),
output(Attr = Val),
!,
report(Items).
report([X|Items]) :-
output(X),
!,
report(Items).
get_av/2 (get attribute value) is the heart of the reasoning engine. It looks for the value of an attribute. If the value isn't already known, then it looks for rules that can be used to compute the value. Those rules might need other attributes, and thus call get_av/2 as well in a recursive reasoning loop.
get_av(Attr, Val) :-
known(Attr, X),
!,
Val = X.
get_av(Attr, Val) :-
rule(Attr, Slots),
get_slot(conditions::Conditions, Slots),
test(Conditions),
get_value(X, Slots),
assert( known(Attr,X) ),
!,
Val = X.
get_av(Attr, Val) :-
F =.. [Attr, X],
formula(F, EQ),
evaluate(EQ),
assert(known(Attr,X)),
!,
Val = X.
get_av(Attr, Val) :-
fuzzy_rules(Attr, Rules),
apply_fuzzy_rules(Rules, CrispVal),
assert(known(Attr,CrispVal)),
!,
Val = CrispVal.
Values in slots might be simple values, or they might require the evaluation of a formula.
get_value(X, Slots) :-
get_slot(value::X, Slots),
!.
get_value(X, Slots) :-
get_slot(formula(X)::EQ, Slots),
evaluate(EQ),
!.
A formula might involve multiple steps. Prolog unification takes care of the variable bindings from step to step.
evaluate([]).
evaluate([EQ|EQs]) :-
call(EQ),
!,
evaluate(EQs).
apply_fuzzy_rules/2 is the heart of the fuzzy part of the system. It takes the rules used to determine an output value, combines all the appropriate fuzzy sets and then defuzzifies the resulting output collection of fuzzy set values. It calls apply_fuzzy_rules/3 with the additional argument used to build the output list.
apply_fuzzy_rules(Rules, CrispVal) :-
apply_fuzzy_rules(Rules, [], FuzzyVals),
defuzzify(Attr, FuzzyVals, CrispVal).
There might be multiple rules for a given fuzzy set. If so the results of those rules are fuzzy or'd together. The result of the predicate is a list of unique fuzzy_set fuzzy_value pairs. For example, [left:0.2, none:0.6].
apply_fuzzy_rules([], SoFar, Results) :-
sort(SoFar, Sorted),
resolve_ors(Sorted, Results),
!.
apply_fuzzy_rules([do(Var)::Rule | Attrs], SoFar, Results) :-
apply_fuzzy_rule(Rule, FuzzyVal),
!,
apply_fuzzy_rules(Attrs, [Var:FuzzyVal | SoFar], Results).
resolve_ors([], []).
resolve_ors([A:V1, A:V2|AVs], Out) :-
max(V1,V2,V),
!,
resolve_ors([A:V|AVs], Out).
resolve_ors([AV|AVs], [AV|Out]) :-
resolve_ors(AVs, Out).
max(X,Y,X) :- X >= Y, !.
max(X,Y,Y).
min(X,Y,X) :- X =< Y, !.
min(X,Y,Y).
A fuzzy rule might be a complex boolean expression. These rules implement the rules for fuzzy and, or, and not. A phrase of a fuzzy rule might contain a hedge, where a hedge is a modifier of a value, such as very. The fuzzify/4 predicate used in the fourth clause gets the fuzzy value in a set from a crisp input value.
apply_fuzzy_rule(C1 fzand C2, FuzzyVal) :-
!,
apply_fuzzy_rule(C1, F1),
apply_fuzzy_rule(C2, F2),
min(F1,F2,FuzzyVal).
apply_fuzzy_rule(C1 fzor C2, FuzzyVal) :-
!,
apply_fuzzy_rule(C1, F1),
apply_fuzzy_rule(C2, F2),
max(F1,F2,FuzzyVal).
apply_fuzzy_rule(fznot C, FuzzyVal) :-
!,
apply_fuzzy_rule(C, F),
FuzzyVal is 1.0 - F.
apply_fuzzy_rule(Attr fzis HedgedVar, HedgedFuzzyVal) :-
get_av(Attr, AttrVal),
strip_hedges(HedgedVar, Var),
fuzzify(Attr, AttrVal, Var, FuzzyVal),
apply_hedges(HedgedVar, FuzzyVal, HedgedFuzzyVal).
strip_hedges(HedgeVar, Var) :-
HedgeVar =.. [Hedge, HVar],
!,
strip_hedges(HVar, Var).
strip_hedges(Var, Var).
apply_hedges(very HVar, Val, HedgedVal) :-
apply_hedges(HVar, Val, HVal),
!,
HedgedVal is HVal * HVal.
apply_hedges(slightly HVar, Val, HedgedVal) :-
apply_hedges(HVar, Val, HVal),
!,
HedgedVal is sqrt(HVal).
apply_hedges(hnot HVar, Val, HedgedVal) :-
apply_hedges(HVar, Val, HVal),
!,
HedgedVal is 1.0 - HVal.
apply_hedges(_, Val, Val).
Given the attribute (Attr), the crisp value (AttrVal) of the attribute, and the name of the fuzzy variable set (Var), compute the fuzzy value. For example, if the fuzzy set cold was defined on temperature as a descending line from 80 degrees to 100, and the temperature was 90,then the fuzzy value would be 0.5.
fuzzify(Attr, AttrVal, Var, FuzzyVal) :-
fuzzy_set(Attr, Vars),
get_slot(variable(Var), SetDefinition, Vars),
fuzz(SetDefinition, AttrVal, FuzzyVal).
Any number of possible shapes of fuzzy sets could be supported. These are the ones supported now.
fuzz(descending_line(X,Y), A, 1.0) :- A =< X, !.
fuzz(descending_line(X,Y), A, 0.0) :- A >= Y, !.
fuzz(descending_line(X,Y), A, B) :- B is (Y-A)/(Y-X), !.
fuzz(ascending_line(X,Y), A, 0.0) :- A =< X, !.
fuzz(ascending_line(X,Y), A, 1.0) :- A >= Y, !.
fuzz(ascending_line(X,Y), A, B) :- B is (A-X)/(Y-X), !.
fuzz(triangle(X,Y,Z), A, 0.0) :- A =< X, !.
fuzz(triangle(X,Y,Z), A, 0.0) :- A >= Z, !.
fuzz(triangle(X,Y,Z), A, B) :- A =< Y, B is (A-X)/(Y-X), !.
fuzz(triangle(X,Y,Z), A, B) :- B is (Z-A)/(Z-Y), !.
fuzz(trapezoid(W,X,Y,Z), A, 0.0) :- A =< W, !.
fuzz(trapezoid(W,X,Y,Z), A, 0.0) :- A >= Z, !.
fuzz(trapezoid(W,X,Y,Z), A, 1.0) :- A >= X, A =< Y, !.
fuzz(trapezoid(W,X,Y,Z), A, B) :- A =< X, B is (A-W)/(X-W), !.
fuzz(trapezoid(W,X,Y,Z), A, B) :- B is (Z-A)/(Z-Y), !.
The tricky part is defuzzification, or the process of taking the fuzzy values of fuzzy variables over a particular domain and converting them to a single real value in the domain. These are the predicates that implement the methods described at the beginning of this section. The two 0 arguments are accumulators for the sum of the area * centroid and the sum of the area.
defuzzify(Domain, FuzzyVals, CrispVal) :-
defuzzify(FuzzyVals, Domain, 0, 0, CrispVal).
I'm not sure this is the most efficient or elegant way to code this. First the points that define the cropped set are determined, and then the generalized centroid calculation that computes the centroid and area under an arbitrary line segment is used. It has the most complicated formula. A better approach might be to use the fact that we know whether a segment defines a rectangle or a right triangle and use the simpler formula for those cases. The predicates supporting those simpler calculations are included, but not actually used.
defuzzify([], _, SumACx, SumA, Crisp) :-
Crisp is SumACx/SumA.
defuzzify([_:0.0|FVs], Domain, SumACx, SumA, Crisp) :-
!,
defuzzify(FVs, Domain, SumACx, SumA, Crisp).
defuzzify([FVar:FVal|FVs], Domain, SumACx, SumA, Crisp) :-
get_points(Domain, FVar, FVal, Points),
centroid(Points, Cx, A),
SumACx2 is SumACx + A*Cx,
SumA2 is SumA + A,
!,
defuzzify(FVs, Domain, SumACx2, SumA2, Crisp).
The predicates that calculate the centroid and area do so from the x,y points that define the line segments of the cropped set. get_points/4 gets those points and returns them in a list, [x1,y1, x2,y2, ...]
get_points(Domain, FVar, FVal, Points) :-
fuzzy_set(Domain, FVars),
get_slot(variable(FVar), FSet, FVars),
set_points(FSet, FVal, Points).
These are the points for the supported fuzzy set shapes. The Ms and Bs in the rules are the slope and y-intercept, derived from the x,y points. In each case, the point list represents a cropped fuzzy set.
set_points(ascending_line(X1,X2), 1.0, [X1,0.0,X2,1.0]) :-
!.
set_points(ascending_line(X1,X2), YVal, [X1,0.0,XVal,YVal,X2,YVal]) :-
M is 1/(X2-X1),
B is -M * X1,
XVal is (YVal-B)/M.
set_points(descending_line(X1,X2), 1.0, [X1,1.0,X2,0.0]) :-
!.
set_points(descending_line(X1,X2), YVal, [X1,YVal,XVal,YVal,X2,0.0]) :-
M is -1/(X2-X1),
B is 1.0 - M * X1,
XVal is (YVal-B)/M.
set_points(triangle(X1,X2,X3), 1.0, [X1,0.0, X2,1.0, X3,0.0]) :-
!.
set_points(triangle(X1,X2,X3), YVal, [X1,0.0, XV1,YVal, XV2,YVal, X3,0.0]) :-
M1 is 1/(X2-X1),
B1 is -M1 * X1,
XV1 is (YVal-B1)/M1,
M2 is -1/(X3-X2),
B2 is 1.0 - M2 * X2,
XV2 is (YVal - B2)/M2.
set_points(trapezoid(X1,X2,X3,X4), 1.0, [X1,0.0, X2,1.0, X3,1.0, X4,0.0]) :-
!.
set_points(trapezoid(X1,X2,X3,X4), YVal, [X1,0.0, XV1,YVal, XV2,YVal, X4,0.0]) :-
M1 is 1/(X2-X1),
B1 is -M1 * X1,
XV1 is (YVal-B1)/M1,
M2 is -1/(X4-X3),
B2 is 1.0 - M2 * X3,
XV2 is (YVal - B2)/M2.
Here are the not-used centroid calculations for the basic shapes. centroid/3 returns the area as well as the centroid for use in the normalized summing process.
centroid(ascending_line(X1,X2,H), Cx, A) :-
Cx is X1 + 2*(X2-X1)/3,
A is H*(X2-X1)/2.
centroid(descending_line(X1,X2,H), Cx, A) :-
Cx is X1 + (X2-X1)/3,
A is H*(X2-X1)/2.
centroid(rectangle(X1,X2,H), Cx, A) :-
Cx is (X2+X1)/2,
A is H*(X2-X1).
This is the messiest centroid, but the most general. It computes the centroid and area under an arbitrary line segment. If the segment is a line, or the edge of a right triangle, this is equivalent to the equations above. I don't know if there's a simpler way to calculate this.
centroid(two_points(X1,Y1,X2,Y2), Cx, A) :-
M is (Y2-Y1)/(X2-X1),
B is Y2 - M * X2,
A is M*X2*X2/2 + B*X2 - M*X1*X1/2 - B*X1,
Mx is M*X2*X2*X2/3 + B*X2*X2/2 - M*X1*X1*X1/3 - B*X1*X1/2,
Cx is Mx/A.
To find the centroid under a list of points, find the centroid under each line segment using the formula given above and then compute the sum of the areas * centroids / sum of the areas.
centroid(PointList, Cx, A) :-
list(PointList),
centroid(PointList, 0, 0, Cx, A).
centroid([_,_], SumACx, A, Cx, A) :-
Cx is SumACx / A,
!.
centroid([X1,Y1,X2,Y2|XYs], SumACx, SumA, Cx, A) :-
centroid(two_points(X1,Y1,X2,Y2), Cx1, A1),
SumACx2 is SumACx + A1*Cx1,
SumA2 is SumA + A1,
!,
centroid([X2,Y2|XYs], SumACx2, SumA2, Cx, A).
Two Knob Shower
The two knob shower is a more complex system. There are independent hot and cold knobs, and it is desired to keep the flow, as well as the temperature, at an optimal level. Here is the control file for it:
fuzzy_set(water_temperature, [
variable(cold) :: descending_line( 80.0, 100.0 ),
variable(just_right) :: triangle( 90.0, 100.0, 110.0 ),
variable(hot) :: ascending_line( 100.0, 120.0 )
]).
fuzzy_set(water_flow, [
variable(low) :: descending_line( 1.5, 2.5 ),
variable(just_right) :: triangle( 2.0, 2.5, 3.0 ),
variable(high) :: ascending_line( 2.5, 3.5 )
]).
fuzzy_set(turn_hot, [
variable(close) :: descending_line( -20.0, 0.0 ),
variable(none) :: triangle( -5.0, 0.0, 5.0 ),
variable(open) :: ascending_line( 0.0, 20.0 )
]).
fuzzy_set(turn_cold, [
variable(close) :: descending_line( -20.0, 0.0 ),
variable(none) :: triangle( -5.0, 0.0, 5.0 ),
variable(open) :: ascending_line( 0.0, 20.0 )
]).
% There are two ways to write the rules for the controls, both are
% equivalent and one is used for hot and the other for cold.
fuzzy_rules(turn_hot, [
do(close) :: water_temperature fzis hot,
do(none) :: water_temperature fzis just_right,
do(open) :: water_temperature fzis cold,
do(close) :: water_flow fzis high,
do(none) :: water_flow fzis just_right,
do(open) :: water_flow fzis low
]).
fuzzy_rules(turn_cold, [
do(open) :: water_temperature fzis hot fzor water_flow fzis low,
do(none) :: water_temperature fzis just_right fzor water_flow fzis just_right,
do(close) :: water_temperature fzis cold fzor water_flow fzis high
]).
rule(water_temperature, [
conditions :: flush = true,
formula(TEMP) :: [
get_av(hot_position, HOT),
get_av(cold_position, COLD),
COLD_ADJUSTED is COLD - 20,
TEMP is (HOT*140 + COLD_ADJUSTED*50) / (HOT + COLD_ADJUSTED) ]
]).
rule(water_temperature, [
conditions :: not flush = true,
formula(TEMP) :: [
get_av(hot_position, HOT),
get_av(cold_position, COLD),
TEMP is (HOT*140 + COLD*50) / (HOT + COLD) ]
]).
rule(water_flow, [
conditions :: flush = true,
formula(FLOW) :: [
get_av(hot_position, HOT),
get_av(cold_position, COLD),
COLD_ADJUSTED is COLD - 20,
FLOW is 2.0*HOT/100 + 2.0*COLD_ADJUSTED/100 ]
]).
rule(water_flow, [
conditions :: not flush = true,
formula(FLOW) :: [
get_av(hot_position, HOT),
get_av(cold_position, COLD),
FLOW is 2.0*HOT/100 + 2.0*COLD/100 ]
]).
rule(flush, [
conditions :: time_ticks > 30 and time_ticks < 40,
value :: true
]).
rule(flush, [
conditions :: true,
value :: false
]).
control(ok, [
conditions :: water_temperature fzis very just_right fzand water_flow fzis very just_right,
actions :: [
update(flush),
update(water_temperature),
update(water_flow),
report([`ok `, tab(2), flush, tab(2), hot_position, tab(2), cold_position, tab(2),
water_temperature, tab(2), water_flow]) ]
]).
control(not_ok, [
conditions :: true,
actions :: [
update(turn_hot, ChangeHot),
update(turn_cold, ChangeCold),
get_av(hot_position, OldHot),
get_av(cold_position, OldCold),
NewHot is OldHot + ChangeHot,
NewCold is OldCold + ChangeCold,
set(hot_position, NewHot),
set(cold_position, NewCold),
update(flush),
update(water_temperature),
update(water_flow),
report([flush, tab(2), hot_position, tab(2), cold_position, tab(2),
water_temperature, tab(2), water_flow]) ]
]).
start(one, [
actions :: [
set(hot_position, 30),
set(cold_position, 30),
set(test_duration, 60),
update(water_temperature),
update(water_flow),
report([`Start test one`, tab(2), hot_position, tab(2), cold_position, tab(2),
water_temperature, tab(2), water_flow]) ]
]).
Links
http://www.depi.itch.edu.mx/apacheco/ai/fuzzy/ - Prof. Al Pacheco's programs and examples implementing fuzzy logic, which were an inspiration for the system described in this newsletter.
http://www.karlscalculus.org/index.shtml - Karl Hahn's excellent calculus tutor, without which I couldn't have cleared the calculus cobwebs from my head.
http://www.quickmath.com/ - A fantastic site that Karl Hahn mentioned that does integrals and other math functions for you.
