Janaury 2004
Errata
It appears for the past few months, my e-mail address has stopped working, so I apologize for ignoring any correspondence during that time. Seeing as it needs fixing, and our Internet guru advises using contact sheets.
For those who asked for the prototype code for the disease interaction system described in the December 2004 newsletter, please ask again. As before, that's a work in progress and I welcome all feedback and comments.
If you're confused on the newsletters, that was due to vacations and some question on the December mailing. December went out as a duplicate in January, and January and February are going out together now.
Eclipse
Eclipse ( http://www.eclipse.org/ ) doesn't really have anything to do with AI. It's an open source integrated development environment (IDE), sponsored by IBM, that is designed to support plug-ins for different languages and tools. Eclipse includes support for projects, smart editors, outliners, cross referencing tools, builds, source code control, local and remote debugging, etc. etc.
Eclipse is written in Java, and, of course has a plug-in for Java development which is very popular with the Java community. Other popular languages are supported plus dozens and dozens of other tools.
That's where it fits into the AI world. All the small vendors and providers of AI tools can now provide a state-of-the-art, platform-independent, development environment for their tools. Last month's issue announced an Eclipse plug-in for Amzi! Prolog. Recently Dr. Ernest J. Friedman-Hill, the author of JESS, a powerful Java rule engine, has been giving interviews in which he discusses the advantages Eclipse will bring to the next JESS release. See the links for an interview with the author of JESS as well a full tutorial on JESS.
Fuzzy Logic
Fuzzy Logic started out as a simple idea that got fuzzier.
The simple idea is that, rather than representing boolean variables with crisp integer values, 1 for true and 0 for false, a real number ranging from 0.0 to 1.0 could be used. It would represent a degree of truth rather than absolute truth or falsehood. Lotfi Zadeh, the creator of modern fuzzy logic, went on to define what all the various logical operations, like ands and ors, mean for fuzzy variables.
The idea gets fuzzy in two dimensions. One, the implementation details get nastier than one might expect; and two, the applicability is not what you might expect.
A Tool for Uncertainty?
At first glance, fuzzy logic seems like an interesting alternative to certainty factors and Bayesian probability for representing uncertainty in rule-based systems, and that is certainly the possibility that generated a lot of early excitement about fuzzy logic. But when you look at a classic kind of uncertain rule:
if symptom is runny_nose then disease is cold
it is not so clear how fuzzy logic would apply. The symptom might have a fuzzy value, and then the rule could have a fuzzy value and the reasoning engine could come up with a fuzzy value for disease is cold. But this has the same type of ad-hoc feel to it that certainty factors have. And probabilities seem like a better way to represent the result anyway.
A Tool for Control Systems!
Whereas it seems difficult and arbitrary to define fuzzy values for something like runny-nosedness, fuzzy variables can be used to make it easier to write rules about attributes that have well-defined ranges of values. For example:
if the water_temperature is hot, turn the control right.
In this case, unlike with the runny nose, there is a well defined number for water temperature, and a well defined number for how far the control might be turned. Rather than write some complex formula that describes the relationship between the two, the use of fuzzy variables, in this case hot and right, lets us express the relationship in a very readable manner.
Where does the fuzziness come in? hot and right represent a degree of hotness and rightness. So the rule captures an infinite range of possibilities. If the water has a high degree of hotness, then the knob will be turned a high degree of rightness; and if there is a small degree of hotness, then only a small degree of rightness.
In other words, if we can come up with a way to define hot and right, and relate them to real numbers like temperature and degrees of rotation of a control knob, and a way to interpret a rule like the one above, then we can come up with a very natural way to write the rules for a control system.
The example rule might come from a shower control system. In a shower with a single knob that is hot to the left and cold to the right a human operator might express expertise in running the shower like this:
if the water_temperature is hot then turn the control right.
if the water_temperature is just_right then turn the control none.
if the water_temperature is cold then turn the control left.
Using fuzzy logic, we could build a rule-based control system for the shower that used rules just like these, without having to resort to a more mathematical approach. The system would iterate to a solution, measuring the temperature, rotating the knob, checking the new temperature, adjusting further, until the desired temperature is reached.
Does that work? Yes, and surprisingly well.
But isn't this really nothing more than interpolation, finding a control motion based on a temperature gradient? Well, yes but the interpolation happens at the beginning and end, when the actual temperature is changed to a fuzzy value for hot, and when the fuzzy value of right is changed back to a degree of rotation. In the middle the rules for propagating and combining fuzzy values take over.
This indirection has a powerful effect. While the shower is a simple example, the rules can become very complex, taking into account many factors. A control engineer doesn't have to worry about the mathematical interactions of many different variables and the equations that govern them, but simply the translation of each individually to and from fuzzy variables. The complex interaction between the variables is dealt with in the uniform domain of the rules for fuzzy logic.
Fuzzy logic is used in numerous real-world control systems, taking complex inputs and using them to adjust the behavior of a system so that it very quickly reaches an optimal state. Examples include braking mechanisms for high speed trains, and docking logic for bringing a ferry smoothly next to a pier. The fuzzyTECH web site in the links has a number of excellent application stories.
It seems like a fuzzy control system would be useful for building a soccer playing robot, so its probably no coincidence that one of the online tutorials on fuzzy logic comes from the Seattle Robotics Society.
How it Works
Let's look at the example of a control system for a shower in more detail. It will take water temperature as an input, and output the degree of rotation of the control knob.
To implement a fuzzy controller, we need to define fuzzy sets for each of the variables. This is where the terminology gets a little confusing. We have a domain variable, say temperature, and then a number of fuzzy sets, like cold, just_right and hot. There could be more, such as perfect, very_hot and the like. But three seems like a good number, so for the shower we can use:
input variable: water_temperature
fuzzy sets: cold, just_right, hot
output variable: rotate
fuzzy sets: left, none, right
Having chosen the sets, the next step is to define them. A fuzzy set definition is a function, often just a straight line, that relates a crisp value to a fuzzy value.
Temperature In
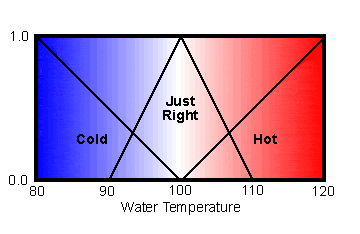
For the shower (yes, we wrote some code and did some experiments with the shower for the Code Corner which will be in the February 2004 newsletter), we decided that 100 degrees is the ideal temperature. Given this, the variables hot and cold would have fuzzy values of 0.0 when the temperature is 100, and values of 1.0 when the temperature is 20 or more degrees different.
The variable just_right will have a peak of 1.0 at 100, and slope off to 0.0 for temperatures 10 degrees on either side. These fuzzy set definitions are illustrated in the diagram to the right.
Knob Rotation Out
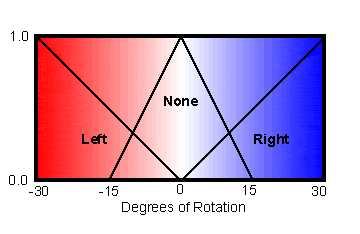
The output is the degrees of rotation of the knob, which can be positioned from from -90 degrees on the left, for hottest, to +90 degrees on the right for coldest. The output rotation is how far to rotate the knob on each iteration.
We chose fuzzy set definitions similar to the temperature ones that allow for a maximum rotation of 30 degrees in either direction.
Importance of Set Definitions
Do these definitions seem arbitrary? Why not move the boundaries around, or even change the curves from straight lines to more logarithmic curves? Well yes they are somewhat arbitrary, but the choices are not as important as you might think. As long as we've got the target temperature in the middle, and somewhat reasonable fuzzy sets, the system will converge relatively efficiently on a just right shower temperature.
Fuzzy systems are very robust, which is why you can add a number of fuzzy variables and still get good performance. But the systems aren't completely indifferent to the input set definitions. My first choice of knob rotation sets led to a system that over controlled the shower, making it too hot, too cold, too hot, etc. But my second set of choices worked just fine.
Illustrating the arbitrariness of it, I just now, while drawing the diagrams, changed the system to use +/- 15 for the none fuzzy set so I wouldn't have to redraw the lines in the pictures. It works just as well as the +/- 10 I originally had.
For some systems getting absolute optimal performance is more important than making it easy to draw the diagrams for an article, and in those cases it is desireable to tune the fuzzy set definitions. What is the best way to tune the sets in an application with many inputs and outputs? It turns our neural nets are excellent tools for tuning fuzzy controllers. We'll leave that for a future newsletter, but some of the articles in the links discuss this, and the fuzzyTECH software supports it.
Fuzzy Control Loop
We now have:
- an input variable and its fuzzy sets,
- an output variable and its fuzzy sets, and
- a set of rules relating the fuzzy values of the input and output fuzzy sets.
A fuzzy control system goes through a loop:
- convert input variables to fuzzy membership values for each set, called fuzzification,
- use the rules to derive fuzzy membership values for the output variable's fuzzy sets, and
- convert the output fuzzy set membership values to a crisp output variable, called de-fuzzification.
Fuzzification
Fuzzification is easy, as it is just picking values from the fuzzy set definitions. You can eyeball the values from the graphs and see, for example, that an input temperature of 96 degrees would be a member of the fuzzy sets defined on temperature to the following degrees:
- cold 0.2
- just_right 0.6
- hot 0.0
In other words, 96 is mostly just_right but is a little cold as well. It's not hot at all.
Apply Rules
The rules relate the input fuzzy set values to the output fuzzy sets. The rules for the single knob shower are simple, and directly relate the three fuzzy sets for control to the corresponding sets for temperature.
if the water_temperature is hot then turn the control right.
if the water_temperature is just_right then turn the control none.
if the water_temperature is cold then turn the control left.
The rules for a fuzzy control system can be much more complex, using boolean operations as defined for fuzzy sets, and dealing with interrelations between a number of variables. But for this simple system and the example input temperature of 96, we get output fuzzy sets like the input ones.
- left 0.2
- none 0.6
- right 0.0
De-Fuzzification (a miracle occurs)
Have you ever seen that cartoon where the scientist has a blackboard full of equations and a little circle in the lower right where he explains "and now a miracle occurs"? That's what happens now for fuzzy logic.
For example one 250+ page book on fuzzy logic with all sorts of details, pictures and equations, when it gets to this step, deals with it in two sentences which basically say: calculate the centroids of each modified membership curve and take the weighted average.
An Internet search for centroids and fuzzy logic yields lots of discussion groups where people are trying to figure out exactly what that means, and very little description.
If you think about the problem of de-fuzzification you'll realize there isn't an obvious best way to do it. We have fuzzy set values of 0.2, 0.6, and 0.0. So clearly we want to move the contol mostly none, but a little bit left. This intuitively corresponds to our sense that we're getting close to the ideal temperature of 100 and so we need just a small adjustment towards hotter, which is to the left. But what computation can we program in a computer that can achieve this intuitive feel?
It turns out there are lots of ways to do it, and, as with other aspects of fuzzy logic, any given method is a bit arbitrary. But the most common method, as the book said, is the weighted average of the centroids. A centroid is the center of gravity of a shape. The shapes are derived by clipping off the tops of fuzzy sets at the membership value.
The solid black areas in the two diagrams below show the shapes that result from clipping the left and none fuzzy sets at their respective values of 0.2 and 0.6.
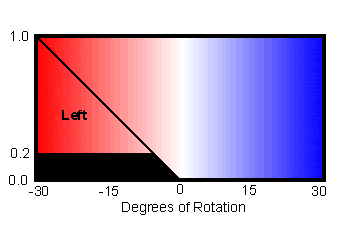
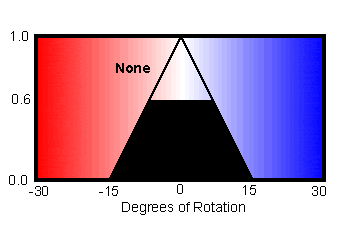
Each of these shapes has a center of gravity and an area. The center of gravity of the left area is a bit left of the -15 degree point. The center of gravity of the none area is 0. These two center of gravity are weighted by the area of each, and then averaged. The result is an answer that will be closer to the none center of gravity than the left's.
The math yields a weighted average of -4.93, a small change toward hotter, just as we would expect.
So here's some math that can be used for de-fuzzification that provides the desired kind of feel. Finding the actual formulas requires more research, and was partially responsible for delays in this newsletter. The details are described in the Code Corner of the February 2004 newsletter which describes the code used for these fuzzy logic experiments.
The Single Knob Shower
To test the idea we simulated a single knob shower, with an initial setting of the dial at 50 degrees. All the way left was pure hot water at 140 degrees, and all the way right was pure cold at 50. So the perfect shower temperature would be with the knob turned to the left somewhat.
The test system was also programmed to only adjust the shower when the water_temperature was less than 0.8 just_right. In other words, it stopped adjusting when it got close enough.
One last wrinkle, the simulation was set so someone would flush the toilet while the shower was on, causing a sudden drop in cold water. When the toilet had refilled, the cold water was available again causing a second disruption in temperature. These changes are seen in iterations 11, where the temperature goes up suddenly, and 20, where the temperature drops.
| Iteration | External Events | Control Angle | Temperature |
|---|---|---|---|
| 0 | 50.00 | 70.00 | |
| 1 | 30.00 | 80.00 | |
| 2 | 10.00 | 90.00 | |
| 3 | -8.33 | 99.17 | |
| 4-10 | -8.33 | 99.17 | |
| 11 | flush | -8.33 | 109.17 |
| 12 | flush | 6.43 | 101.78 |
| 13-19 | flush | 6.43 | 101.78 |
| 20 | 6.43 | 91.78 | |
| 21 | -5.46 | 97.73 | |
| 22 | -8.37 | 99.18 | |
| 23 | -8.37 | 99.18 |
Notice that in the beginning it took four iterations to reach a just_right temperature. The first three roations were 20 degrees, which is less than the maximum 30 degrees. This is because of the mysterious de-fuzzification algorithm using centroids. A full left turn is defuzzified at the center of gravity of the left fuzzy set, which is -20 degrees.
By adding extra fuzzy sets, such as very cold and very hot and alot left and alot right, we can get the system to use more dramatic changes when a larger adjustment is needed. We can also define and use the modifiers "very" and "alot" and make them part of the fuzzy set definitions. Typically "very" is defined as the square of a fuzzy value, so, for example, 0.8 cold would be 0.64 very cold. That is, a temperature is not as "very cold" as it is "cold".
Notice that the ten degree changes in temperature caused by first flushing a toilet, and then having the toilet finish filling, were both accomodated for in one or two iterations.
Two Knob Shower
We did a second shower system for a shower with two knobs, one for hot and one for cold, and added the constraint that we would like to get a total flow of 2.5 gallons/minute.
This meant having two input variables, water_temperature and water_flow, and two outputs for the hot and cold controls. The outputs were expressed in terms of open/close instead of left/right. Because there were two controls, we needed two sets of rules, one for each control.
if temperature is hot then hot_control close
if temperature is just_right than hot_control none
if temperature is cold then hot_control open
if flow is high then hot_control close
if flow is just_right then hot_control none
if flow is low then hot_control open
We used separate rules for the different conditions above. Fewer rules using fuzzy boolean operations are also possible. Below we use an equivalent set of rules that make use of fuzzy boolean operators.
if temperature is hot or flow is low then cold_control open
if temperature is just_right or flow is just_right then cold_control none
if temperature is cold or flow is high then cold_control close
This slightly more complex system shows the power of fuzzy control systems. Adding definitions for flow and the two controls as we did for the single control shower, and the rules exactly as written above, we had a system that very quickly dealt with the sometimes contradictory requirements of flow and temperature to produce just_right temperature and flow.
No tuning was necessary, and the results here are those from the first try. This illustrates the tremendous power of fuzzy control systems. With relatively little work a complex system with good performance can be implemented. Compare this approach to trying to derive a more mathematical one for adjusting both flow and temperature with the two knobs.
Here are the results, and, as with the single knob shower, we introduced a flush of the toilet that, in this case, removed cold water from the system and reduced the flow. See iterations 31 and 40 for the effects.
| Iteration | External Events | Hot Position | Cold Position | Temperature | Flow |
|---|---|---|---|---|---|
| 0 | 30.00 | 30.00 | 95.00 | 1.20 | |
| 1 | 39.69 | 34.65 | 98.05 | 1.48 | |
| 2 | 48.69 | 41.49 | 98.59 | 1.80 | |
| 3 | 57.05 | 48.19 | 98.78 | 2.10 | |
| 4 | 63.70 | 53.23 | 99.02 | 2.34 | |
| 5 | 67.73 | 55.74 | 99.37 | 2.47 | |
| 6-30 | 67.73 | 55.74 | 99.37 | 2.47 | |
| 31 | flush | 67.73 | 55.74 | 108.91 | 2.07 |
| 32 | flush | 67.57 | 65.86 | 103.61 | 2.27 |
| 33 | flush | 68.40 | 71.24 | 101.45 | 2.39 |
| 34 | flush | 69.22 | 74.32 | 100.42 | 2.47 |
| 35-39 | flush | 69.22 | 74.32 | 100.42 | 2.47 |
| 40 | 69.22 | 74.32 | 93.34 | 2.87 | |
| 41 | 68.72 | 66.34 | 95.79 | 2.70 | |
| 42 | 68.87 | 61.13 | 97.67 | 2.60 | |
| 43 | 69.22 | 57.82 | 99.03 | 2.54 | |
| 44 | 69.22 | 57.82 | 99.03 | 2.54 |
The more complex system takes three or four iterations to get to just_right to a degree of 0.8 for both flow and temperature.
Serotonin Syndrome
If you remember, the topic of fuzzy logic began with a search for a way to represent the uncertainty in the rules describing the serotonin syndrome. At first fuzzy logic good, but then it seemed more useful for control systems. But wait, isn't the description of the serotonin syndrome really one of a control system? There are cells emitting serotonin and the blood stream reacting to the serotonin, and these are controlled by inputs of various drugs. Maybe a fuzzy model of the control mechanism of serotonin is exactly what the doctor ordered.
Links
http://ai-depot.com - The AI Depot is a site loaded with tutorials, essays and other goodies related to AI.
http://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol4/sbaa/report.html - Shahariz Abdul Aziz and Jeyakody Parthiban tutorial on fuzzy sets, rules and conrol systems, with an interesting case study dealing with traffic lights. It contains, at the end, a list of other tutorials on fuzzy logic.
http://www.austinlinks.com/Fuzzy/tutorial.html - James F Brule's tutorial on fuzzy systems.
http://www.seattlerobotics.org/encoder/mar98/fuz/flindex.html - The Seattle Robotics Society's tutorial on fuzzy logic.
http://www.depi.itch.edu.mx/apacheco/ai/fuzzy/ - Prof. Al Pacheco's programs and examples implementing fuzzy logic.
http://www.karlscalculus.org/index.shtml - Karl Hahn's excellent calculus tutor, without which I couldn't have cleared the calculus cobwebs from my head.
http://www.quickmath.com/ - A fantastic site that Karl Hahn mentioned that does integrals and other math functions for you.
http://www.fuzzytech.com/ - fuzzyTECH's home page, a commercial vendor of fuzzy and neuro-fuzzy tools. It includes a number of excellent application stories.
http://www.cs.vu.nl/~ksprac/2002/doc/Jess60/index.html - A tutorial on JESS, including some good material on the Rete algorithm.
http://www.devx.com/Java/Article/17651 - An interview with Dr. Ernest J. Friedman-Hill, the author of JESS, which discusses, among other things, the upcoming Eclipse plug-in.
